Data-Centric Parallel Programming
Decoupling domain science from performance optimization.
The DAPP project aims to build new representations for programs and algorithms, in order to efficiently map them to the entire hardware architecture landscape (CPU, GPU, and FPGA) with high utilization. With data-centric parallel programming, we enable direct knowledge transfer of performance optimization, regardless of the scientific application or the target processor.
Publications
- Productive Performance Engineering for Weather and Climate Modeling with Python
Tal Ben-Nun, Linus Groner, Florian Deconinck, Tobias Wicky, Eddie Davis, Johann Dahm, Oliver Elbert, Rhea George, Jeremy McGibbon, Lukas Trümper, Elynn Wu, Oliver Fuhrer, Thomas Schulthess, Torsten Hoefler. To appear at Supercomputing 2022. Paper - Boosting Performance Optimization with Interactive Data Movement Visualization
Philipp Schaad, Tal Ben-Nun, Torsten Hoefler. To appear at Supercomputing 2022. Paper - Deinsum: Practically I/O Optimal Multilinear Algebra
Alexandros Nikolaos Ziogas, Grzegorz Kwasniewski, Tal Ben-Nun, Timo Schneider, Torsten Hoefler. To appear at Supercomputing 2022. Paper - Temporal Vectorization: A Compiler Approach to Automatic Multi-Pumping
Carl-Johannes Johnsen and Tiziano De Matteis and Tal Ben-Nun and Johannes de Fine Licht and Torsten Hoefler. To appear at ICCAD 2022. Paper - A data-centric optimization framework for machine learning
Oliver Rausch, Tal Ben-Nun, Nikoli Dryden, Andrei Ivanov, Shigang Li, Torsten Hoefler. ICS 2022. Paper - Lifting C semantics for dataflow optimization
Alexandru Calotoiu, Tal Ben-Nun, Grzegorz Kwasniewski, Johannes de Fine Licht, Timo Schneider, Philipp Schaad, Torsten Hoefler. ICS 2022. Paper - Productivity, Portability, Performance: Data-Centric Python
Alexandros Nikolaos Ziogas, Timo Schneider, Tal Ben-Nun, Alexandru Calotoiu, Tiziano De Matteis, Johannes de Fine Licht, Luca Lavarini, Torsten Hoefler. Supercomputing 2021. Paper - Pebbles, Graphs, and a Pinch of Combinatorics: Towards Tight I/O Lower Bounds for Statically Analyzable Programs
Grzegorz Kwasniewski, Tal Ben-Nun, Lukas Gianinazzi, Alexandru Calotoiu, Timo Schneider, Alexandros Nikolaos Ziogas, Maciej Besta, Torsten Hoefler. SPAA 2021. Paper - Data Movement Is All You Need: A Case Study on Optimizing Transformers
Andrei Ivanov, Nikoli Dryden, Tal Ben-Nun, Shigang Li, Torsten Hoefler. MLSys 2021. Outstanding Paper Award. Paper - StencilFlow: Mapping large stencil programs to distributed spatial computing systems
Johannes de Fine Licht, Andreas Kuster, Tiziano De Matteis, Tal Ben-Nun, Dominic Hofer, Torsten Hoefler. CGO 2021. Paper - A Data-Centric Approach to Extreme-Scale Ab initio Dissipative Quantum Transport Simulations
Alexandros Nikolaos Ziogas, Tal Ben-Nun, Guillermo Indalecio Fernández, Timo Schneider, Mathieu Luisier, Torsten Hoefler. Supercomputing 2019. Won ACM Gordon Bell Prize. Paper - Optimizing the Data Movement in Quantum Transport Simulations via Data-Centric Parallel Programming
Alexandros Nikolaos Ziogas, Tal Ben-Nun, Guillermo Indalecio Fernández, Timo Schneider, Mathieu Luisier, Torsten Hoefler. Supercomputing 2019. Paper - Stateful Dataflow Multigraphs: A Data-Centric Model for High-Performance Parallel Programs
Tal Ben-Nun, Johannes de Fine Licht, Alexandros Nikolaos Ziogas, Timo Schneider, Torsten Hoefler. Supercomputing 2019. Paper | Slides | Video
DaCe
The Data-Centric (DaCe) programming paradigm is a project that revolutionizes the way we see programming, in order to cope with the challenges that computational sciences are facing today. In particular, modern computer architectures are diverse and change every few years, to the point where buying a new computer does not simply accelerate computation. Rather, the underlying code has to change every time to adapt, and the burden is on the scientists. This is affecting many fields, from computational chemistry to machine learning, slowing down progress in research.
DaCe aims to change the process of code adaptation by defining a flow-based graph representation for programs, called the Stateful Dataflow Multigraph (SDFG). This same representation can generate high-performance programs for Intel/IBM/Arm CPUs, NVIDIA/AMD GPUs, Intel/Xilinx FPGAs, custom processors, and clusters thereof. DaCe programs are on par and outperform the existing state-of-the-art on all of these platforms. To aid the code optimization process, DaCe provides the programmers with visual transformation and editing tools, right in the Visual Studio Code integrated development environment. Several languages and frameworks can be compiled with DaCe, including Python/NumPy, PyTorch and ONNX (via DaCeML), and a subset of MATLAB.
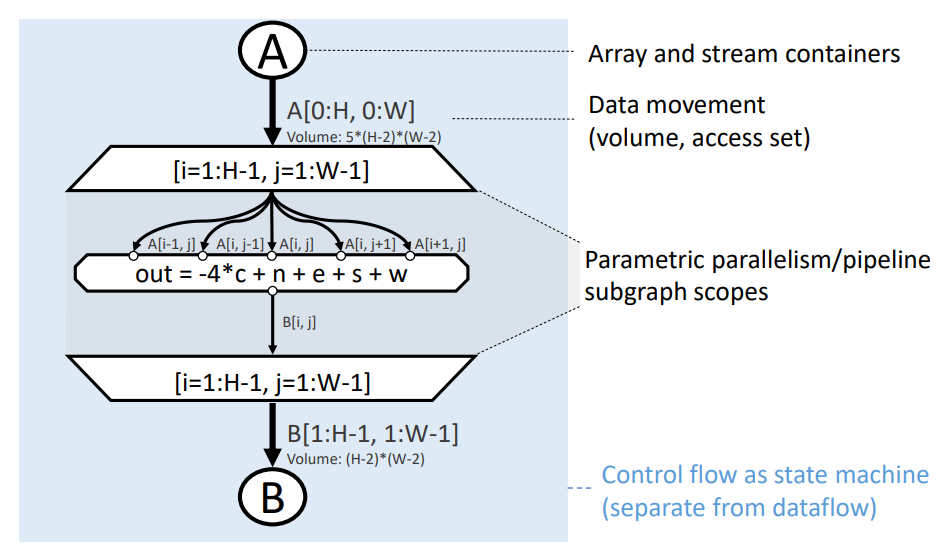
The data-centric SDFG representation
Below we see a naive matrix multiplication in a declarative form, using the DaCe numpy interface, and the resulting SDFG:
@dace.program
def gemm(A: dace.float64[M, K], B: dace.float64[K, N],
C: dace.float64[M, N]):
# Transient variable
tmp = numpy.empty([M, N, K], dtype=A.dtype)
for i, j, k in dace.map[0:M, 0:N, 0:K]:
tmp[i, j, k] = A[i, k] * B[k, j]
C[:] = numpy.sum(tmp, axis=2)In the graph, the blue region represents one state in the state machine. Circular nodes (A, B, tmp, C) are Arrays, hexagons (mult) are code Tasklets, the triangle represents reduction, and the edges represent the data moved between the nodes. To explicitly mark and enable parametric parallelism, SDFGs define Map scopes (between the trapezoid nodes) with ranges.
The above version consumes N*M*K additional memory for tmp, which is not scalable. If we run the script, however, DaCe can transform the SDFG by fusing the map and reduce nodes, as follows:
$ python3 gemm.py
==== Program start ====
Matrix multiplication 1024x1024x1024
Automatically applied 2 strict state fusions and removed 0 redundant arrays.
0. Pattern FPGATransformCubed in gemm
...
8. Pattern MapReduceFusion in 3 -> 4 -> 5
...
Select the pattern to apply (0 - 11 or name$id): 8
You selected (8) pattern MapReduceFusion in 3 -> 4 -> 5 with parameters {}
We then obtain the following SDFG, which can also be manually programmed in Python (left-hand side).
@dace.program
def gemm(A: dace.float64[M, K], B: dace.float64[K, N],
C: dace.float64[M, N]):
for i, j, k in dace.map[0:M, 0:N, 0:K]:
C[i, j] += A[i, k] * B[k, j]The same thing can be done directly in Visual Studio Code:
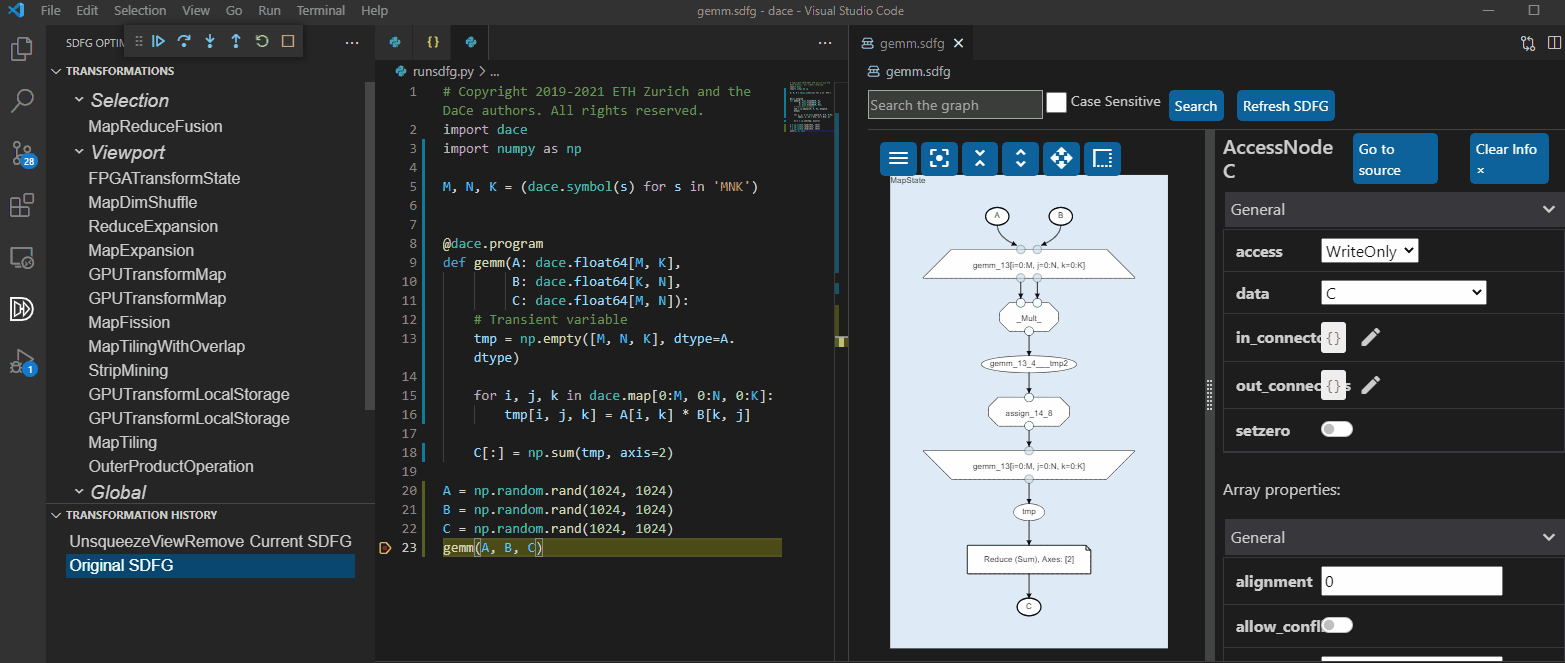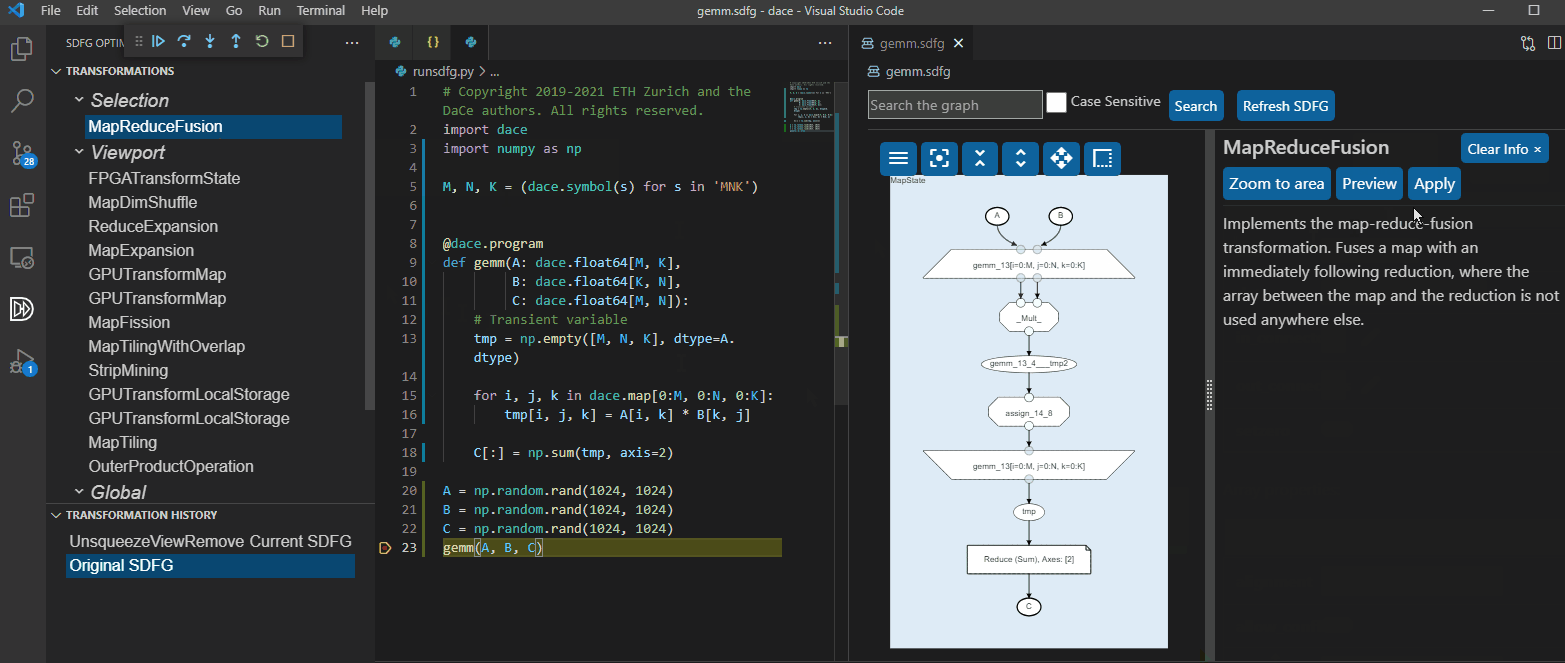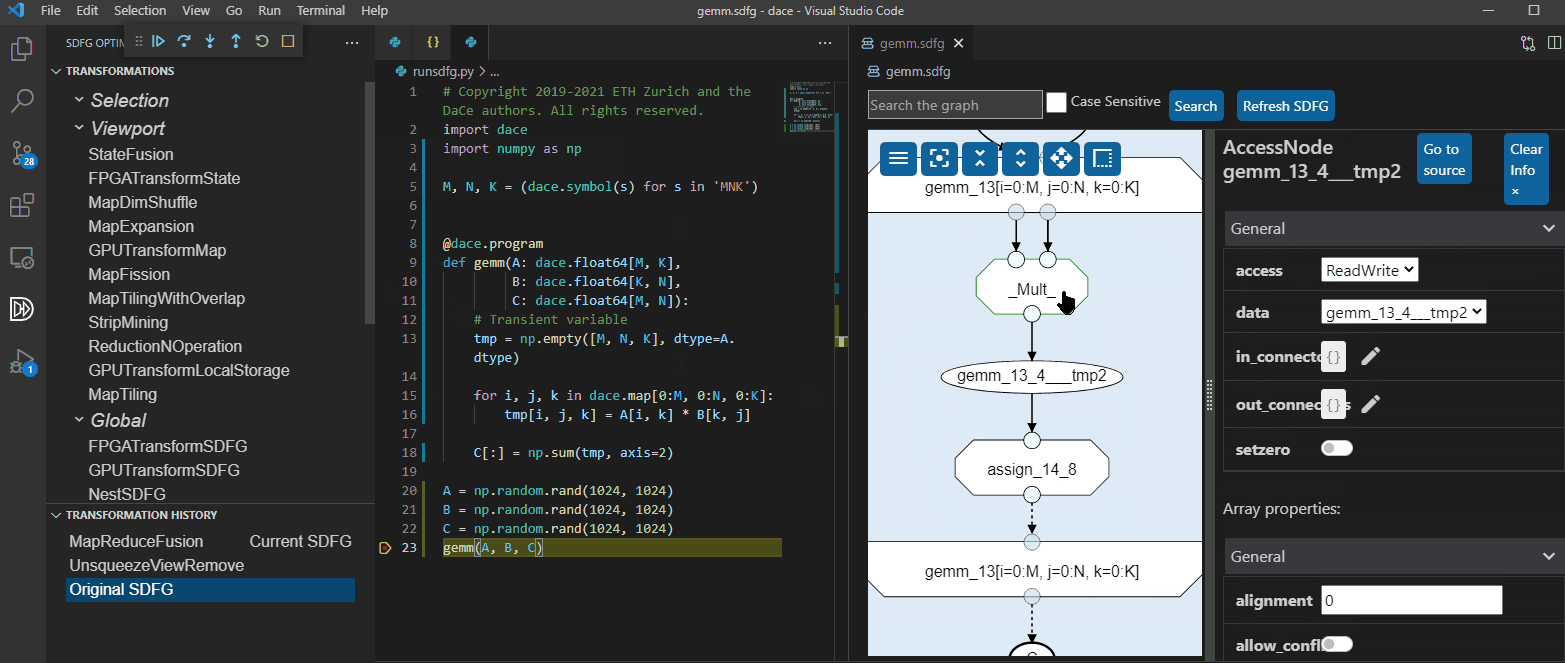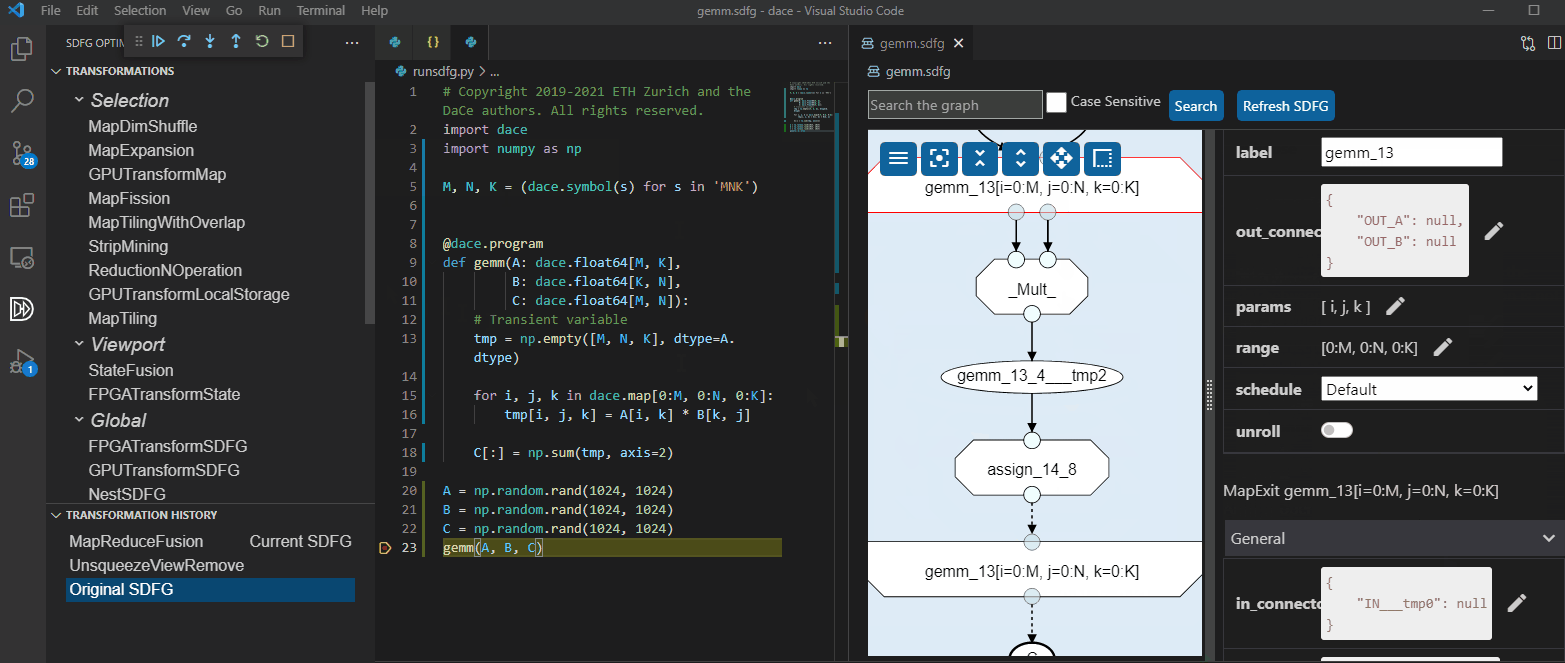
Transforming the graph, both manually and automatically, can yield performance that is 98.6% of Intel MKL on CPU, 90% of NVIDIA CUTLASS on GPU, and 4,992x faster than High-Level Synthesis using Xilinx SDAccel on FPGA (see Performance for more results). An implicit matrix multiplication produces a reasonably fast version automatically:
@dace.program
def gemm(A: dace.float64[M, K], B: dace.float64[K, N], C: dace.float64[M, N]):
C = A @ BPerformance
Fundamental Kernels
These are the runtimes of DaCe compiled from SDFGs on different fundamental computational kernels: Query with a predicate, Matrix Multiplication (MM), Histogram, 2D Jacobi Stencil, and Sparse Matrix-Vector multiplication (SpMV). We test CPUs, GPUs, and FPGAs.
Intel Xeon E5-2650 v4 (12 cores)
NVIDIA Tesla P100
Xilinx XCVU9P FPGA
Quantum Transport Simulation
We use DaCe to optimize the computation and communication of the OMEN quantum transport simulator. Over the previous, manually optimized state-of-the-art implementation, DaCe-OMEN exhibits a ~140x speedup. Due to the data-centric approach, it became apparent that the communication scheme could scale better if the code would undergo data movement transformations. Normally, this would cause a complete rewrite of the codebase, but with DaCe it is a matter of applying transformations:
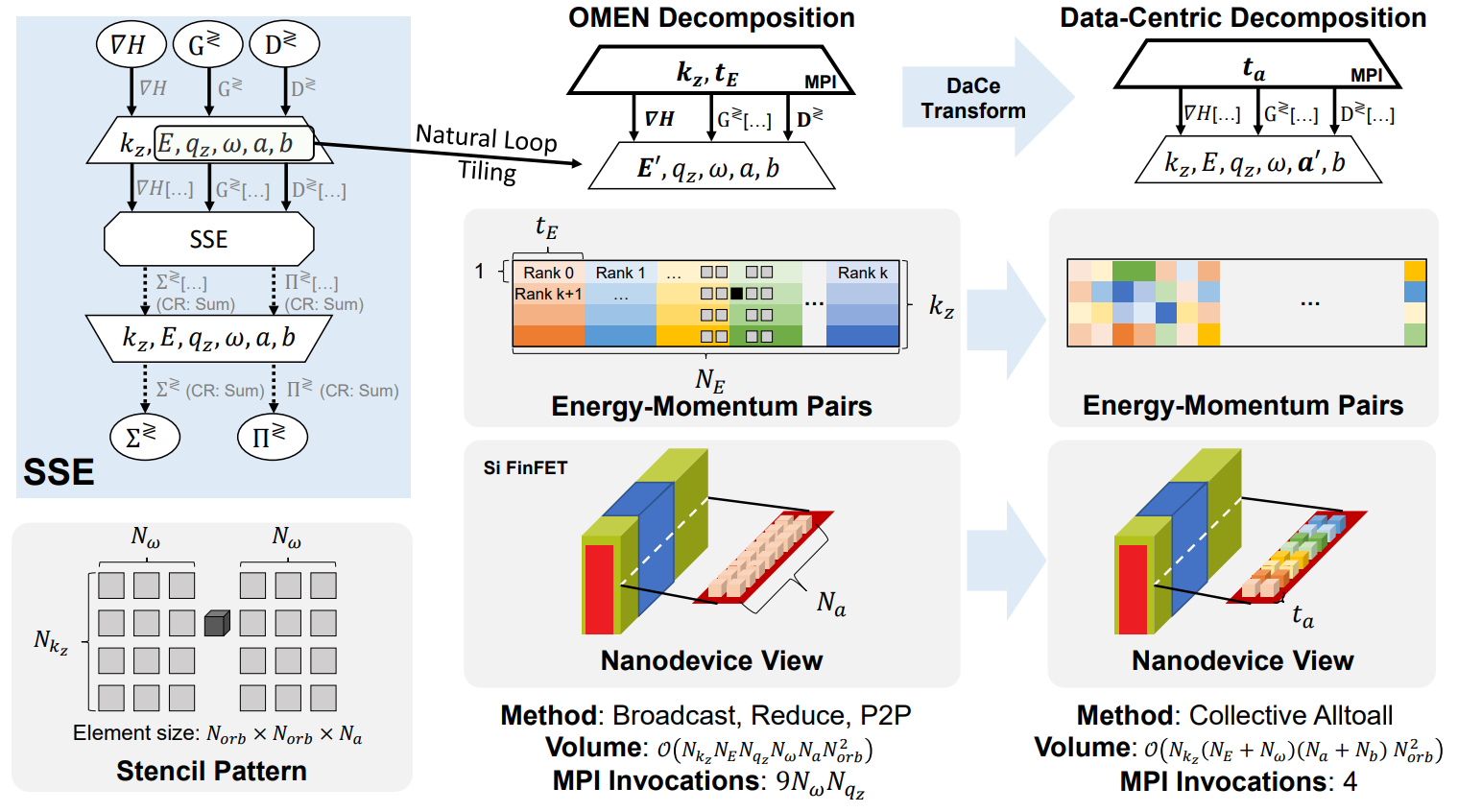
By using the same data-centric transformations on the operator level as well (more details can be found in the paper), we were able to achieve speedups of 5.76-31x over NVIDIA's optimized CUBLAS library. Putting all the pieces together, DaCe-OMEN scaled to the full Summit supercomputer, achieving simulation of numbers of atoms that were not possible to simulate before.
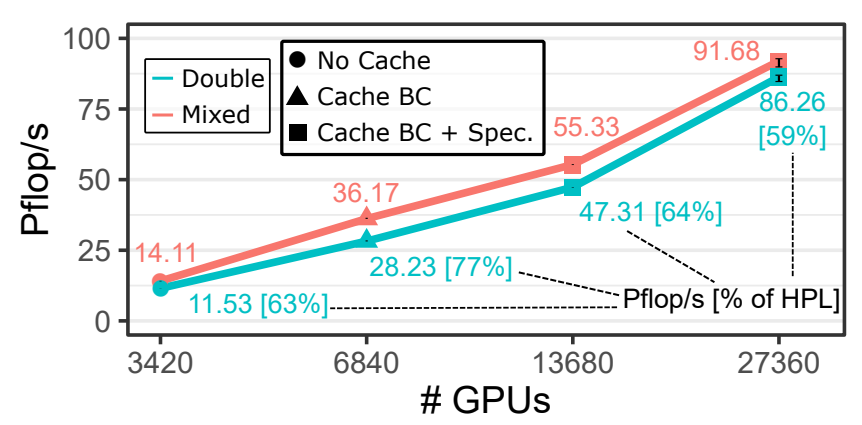
DaCe-OMEN strong scaling with 10,240 atoms on the Summit supercomputer
This effort won the ACM Gordon Bell Prize in 2019.
Team

Johannes de Fine Licht

Alexandros-Nikolaos Ziogas

Timo Schneider



