Slim Fly: A Cost Effective Low-Diameter Network Topology
The key idea in a single sentence
"It's ALL about the diameter!": Optimize your topology for low diameter to not only reduce the latency (due to shorter paths) but also cost and power consumption as packets will traverse and thus require fewer routers and cables.
Key motivation
Interconnection networks play an important role in today's large-scale computing systems. An ideal topology should ensure: high bandwidth, low total system cost and energy consumption, low endpoint-to-endpoint latency, and resiliency to link failures. We develop the Slim Fly topology that achieves all these goals by lowering the diameter.
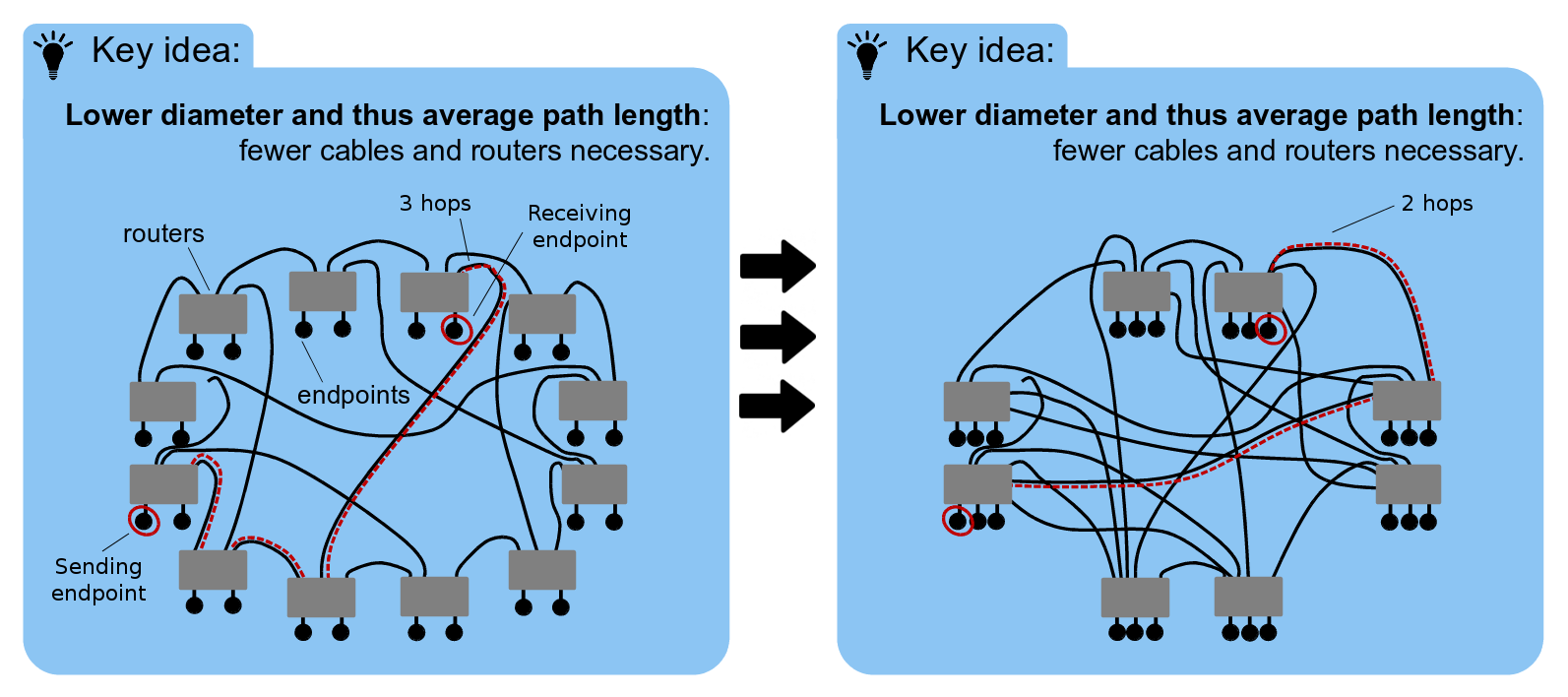
The key idea and motivation: On the left, a topology has a diameter of 3; two communicating endpoints require 3 hops. On the right, the topology has been rearranged so that the diameter is 2. Thus, packets require fewer routers and cables, which reduces dynamic power (fewer SerDes traversed), static power (fewer powered resources) and the cost (less equipment). At the same time, the endpoint density was increased to preserve the number of endpoints. Here, we take advantage of today's technological advances that enable cheap manufacturing of high-radix routers.
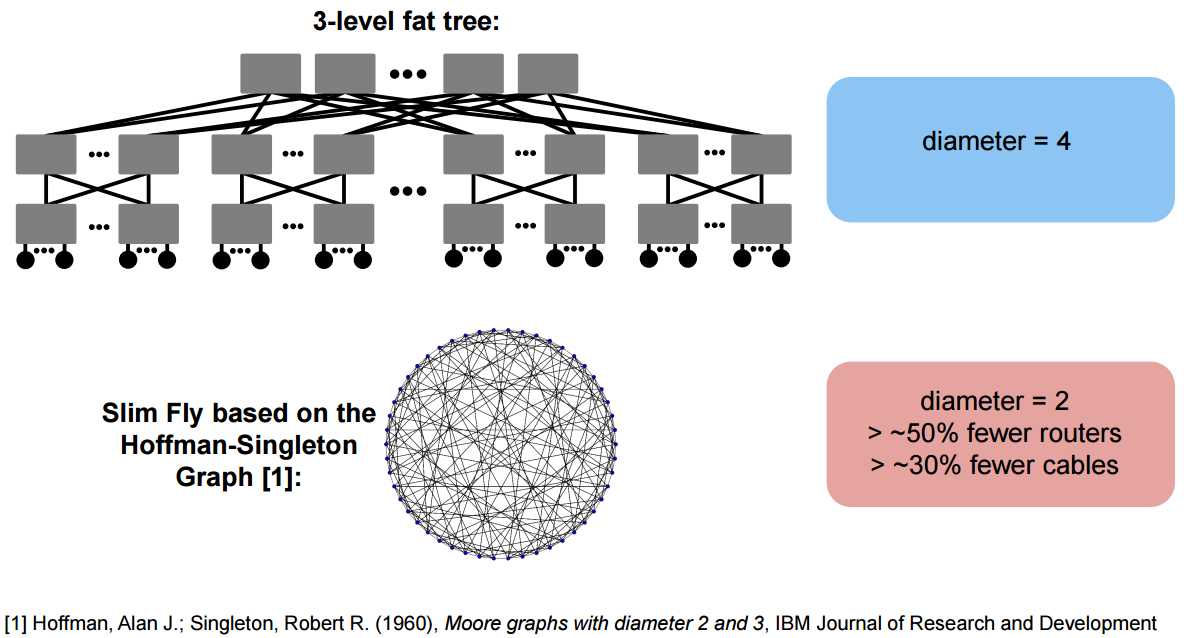
A comparison between a full-bandwidth fat tree and a Slim Fly: Both topologies offer high bandwidth, while SF reduces the number of routers (>50%) and cables (>30%).
Key method (of lowering the diameter)
We optimize the structure of Slim Fly towards the Moore Bound, a well-known
concept in graph theory; see a figure below for an overview. The Moore Bound
(MB) determines the maximum number of vertices that a potential graph with a
given vertex degree and diameter can have. We use the MB concept in our
construction scheme and we define it to be the upper limit on the number of
radix-k routers that a network with a given diameter D can contain. To
connect the routers, we first fix D and k, and then use/construct graphs with these D and
k that are close to the MB. We focus on D=2 (but also briefly analyze D=3) and we select k to match the radix
of available routers. In this way, we maximize the number of attached
endpoints for a given D and k. This minimizes the cost per endpoint:
intuitively, using graphs close to the MB enables the Slim Fly network to be
as "inflated" with endpoints as possible for a given D and k, thus minimizing
cost/power consumption per endpoint.
If you want to see in more detail how to connect the routers in a Slim Fly, scroll down to the section "Constructing Slim Fly".
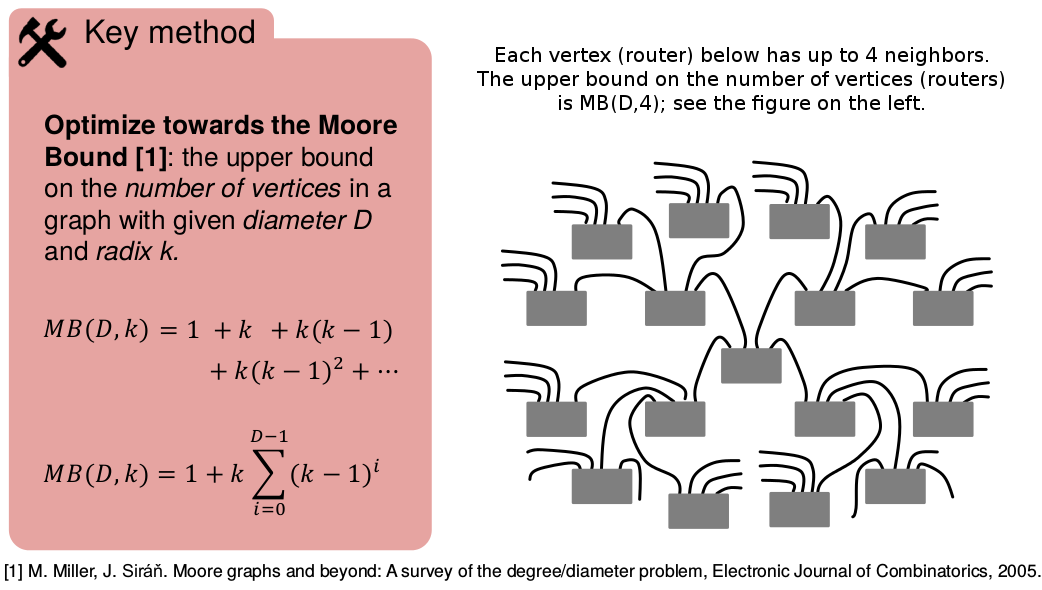
The notion of Moore Bound in more detail.
Key method (of attaching the endpoints)
We select the number of endpoints p attached to one router to
maximize the total cumulative throughput (i.e., the global bandwidth) in the all-to-all
communication pattern. We select all-to-all because this is
a common traffic pattern in various HPC and Big Data codes.
We derive p by modeling analytically the average amount
of traffic in the all-to-all pattern and then ensuring that both injection
links and router-to-router links bear the same amount of traffic (balancedness).
If you want to see in more detail how to attach the endpoints in a Slim Fly, scroll down to the section "Constructing Slim Fly".
Constructing Slim Fly
We present an intuitive high-level description of Slim Fly's structure below. The full description is in the paper and also in the slides; references and links are at the bottom of the page.
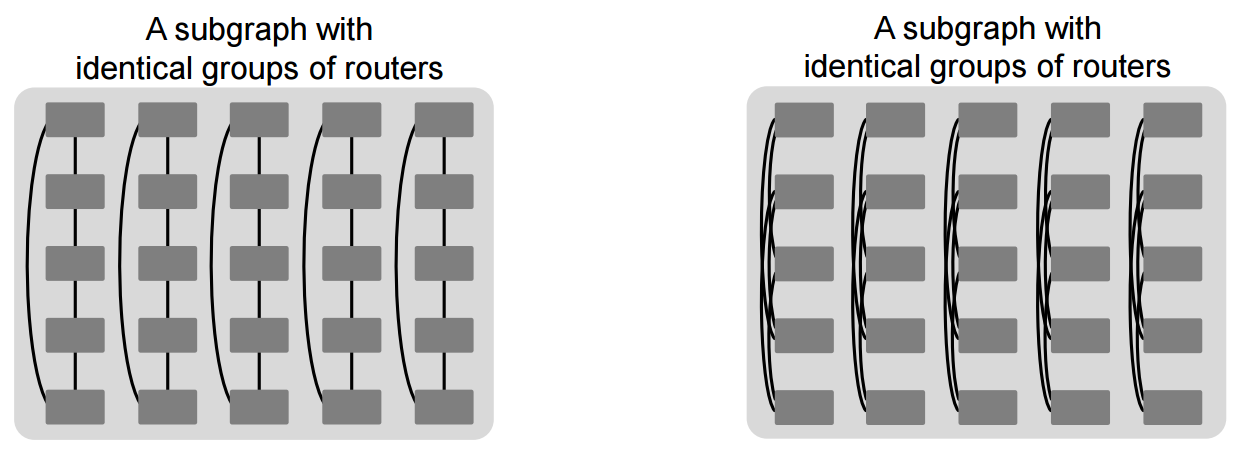
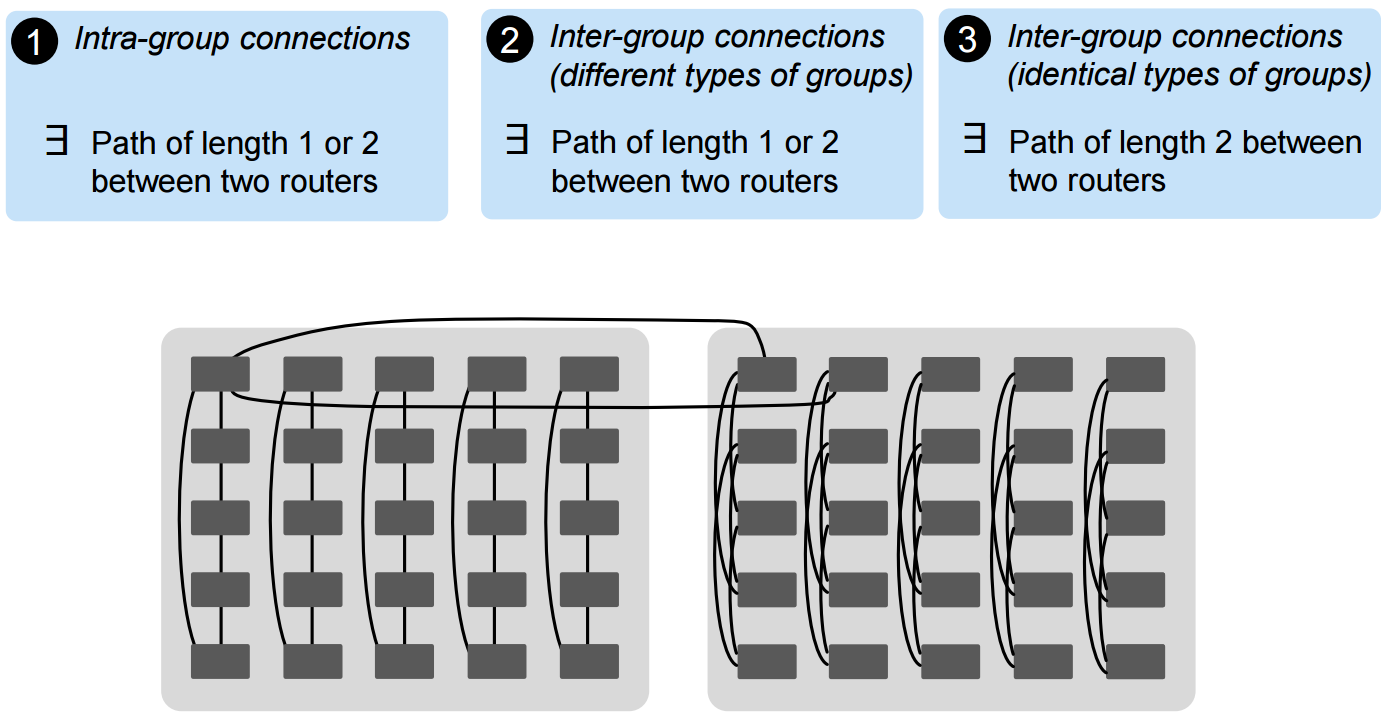
The structure of Slim Fly: part 1: Each Slim Fly consists of two subgraphs. Each of these two subgraphs consists of the same number of groups of routers. Within one subgraph, there are cables within each group, but the groups are not connected with one another. The cabling pattern in each group (in one subgraph) is identical, and usually different from the cabling pattern inside groups in the other subgraph.
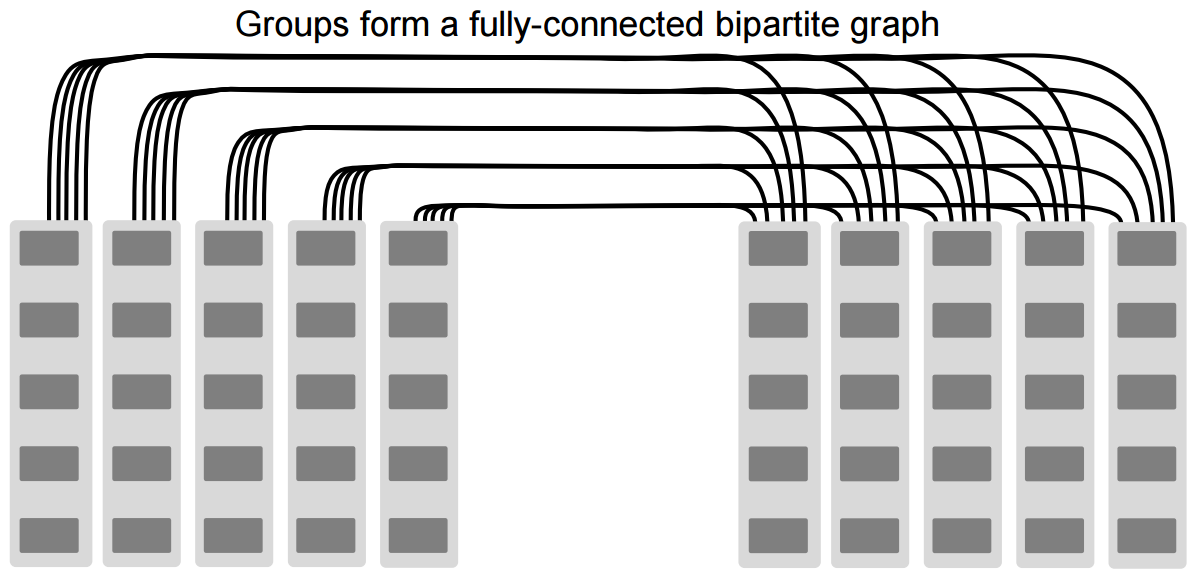
The structure of Slim Fly: part 2: Groups are heavily connected across the subgraphs. They form a fully-connected bipartite graph (i.e., each group in one subgraph is connected to all the other groups in the other subgraph).
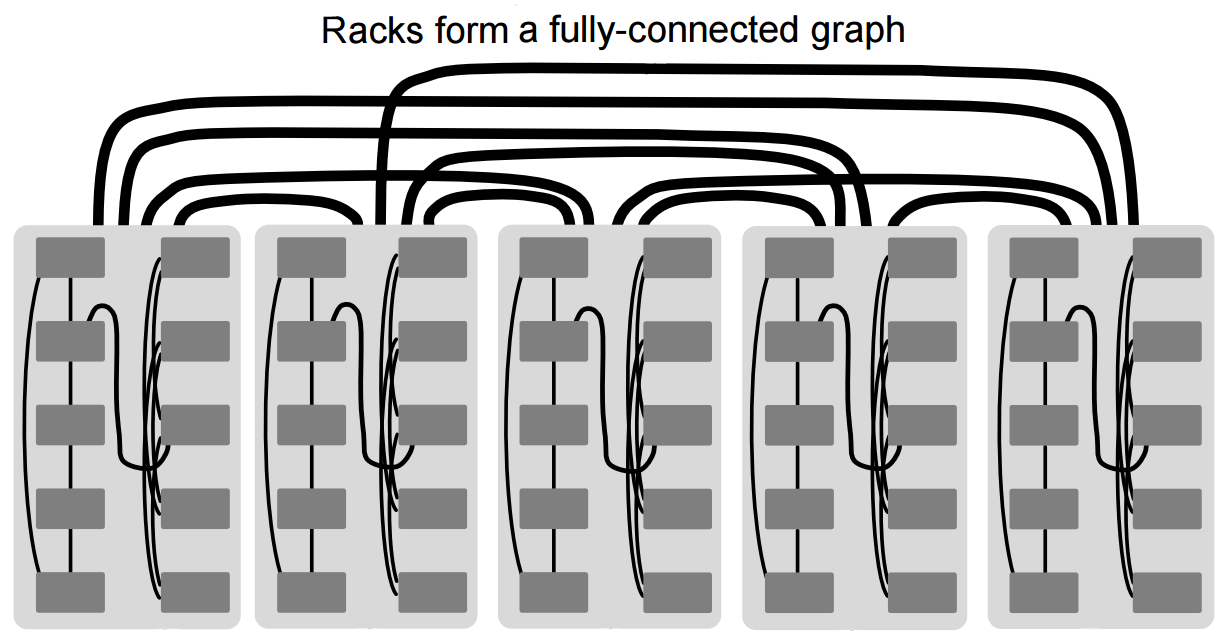
The structure of Slim Fly: part 3: For a simpler layout (e.g., in a data center), groups from different subgraphs can be rearranged and merged pairwise. As a result, such Slim Fly consists of identical racks and each rack has the same intra-rack cabling pattern. Racks form a fully-connected grapg (i.e., each rack is connected to all the other other racks).
Key findings and discoveries
- Low diameter is the key: lowering the diameter reduces the latency as well as the cost and power consumption. The Slim Fly with diameter 2 preserves high bandwidth and outperforms all the comparison targets (both low-radix traditional networks and state-of-the-art high-radix designs) in cost, power consumption, and latency.
- Moore Graphs ensure desired network properties: in addition to the above, graphs that approach the Moore Bound ensure high bandwidth and resilience. They also have structure of connections that allows for a data center or supercomputer rack-based layout.
Selected interesting analyses
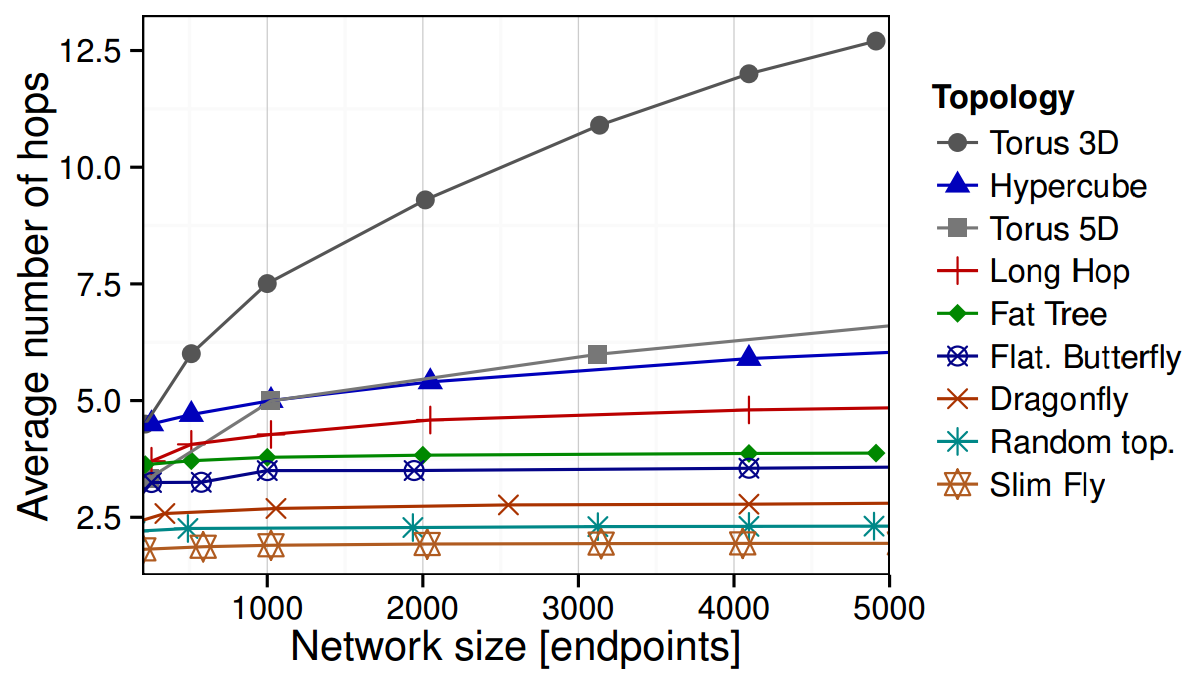
Average path length: Slim Fly offers the lowest one.
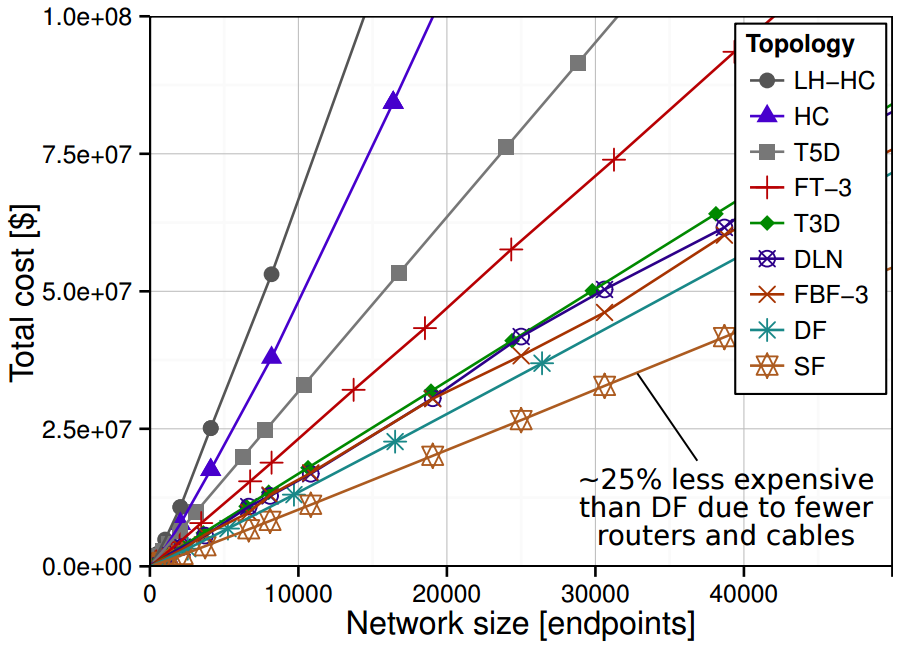
Total network cost (routers + cables): Slim Fly offers the lowest one (25-30% better than that of Dragonfly). Power consumption follows fimilar trends. SF: Slim Fly, DF: Dragonfly, FBF-3: Flattened Butterfly (3 dimensions), DLN: random topologies, T3D: 3d torus, FT-3: a 3-level fat tree, T5D: 5d torus, HC: hypercube, LH: Long Hop.
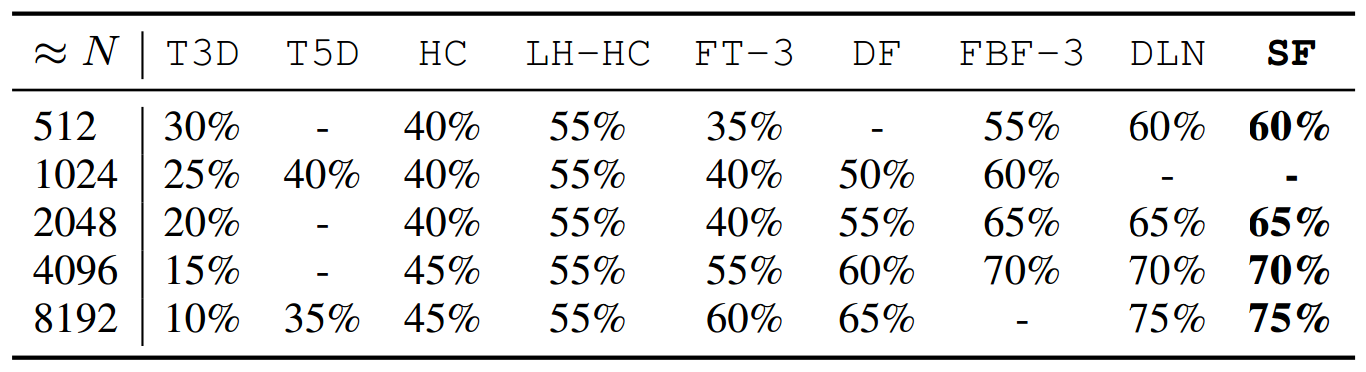
The resilience to link failures: N is the number of endpoints. Network symbols are the same as in the cost analysis above. "-" indicates the lact of a specific network for a given size. Percentages are the numbers of link failures that are required to disconnect the network.
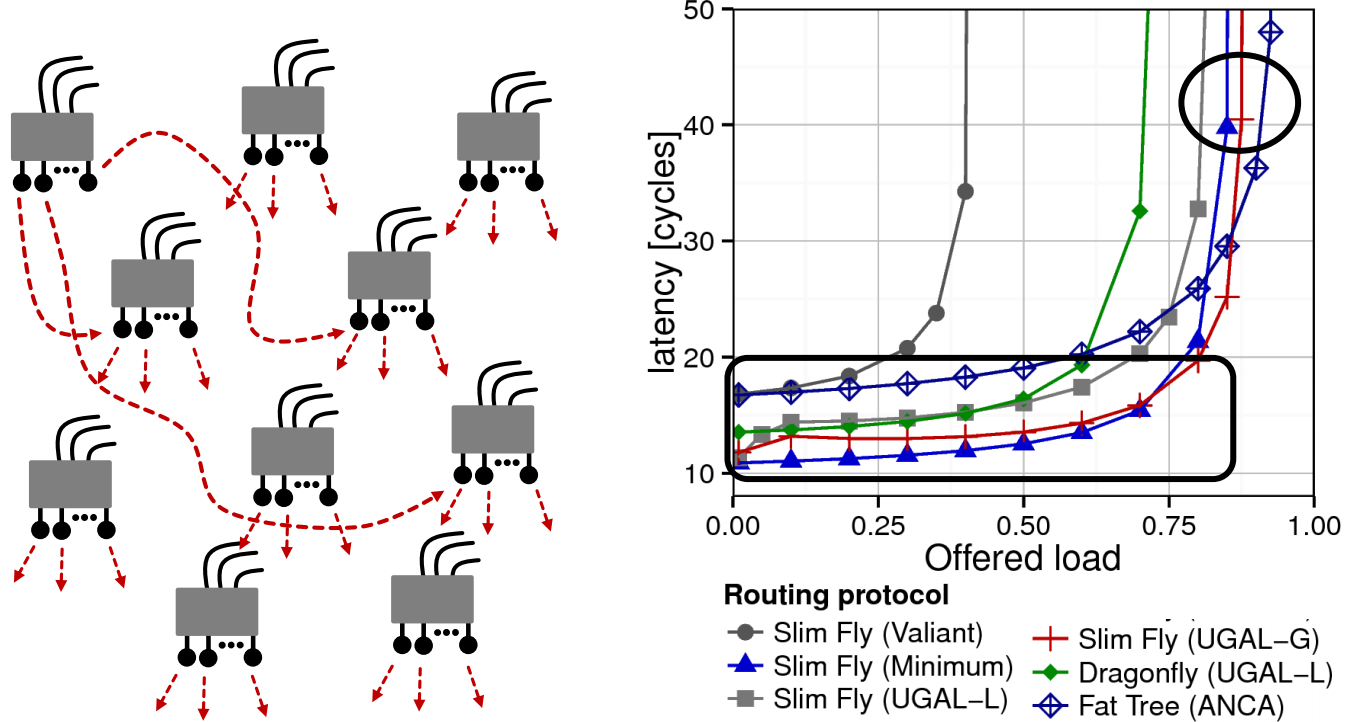
Performance: The latency for a random uniform traffic pattern.
Routing
We propose both minimum static and non-minimum adaptive routing schemes. Each scheme comes with deadlock-freedom guarantees. Again, check the paper for all the details.
Minimum static routing.
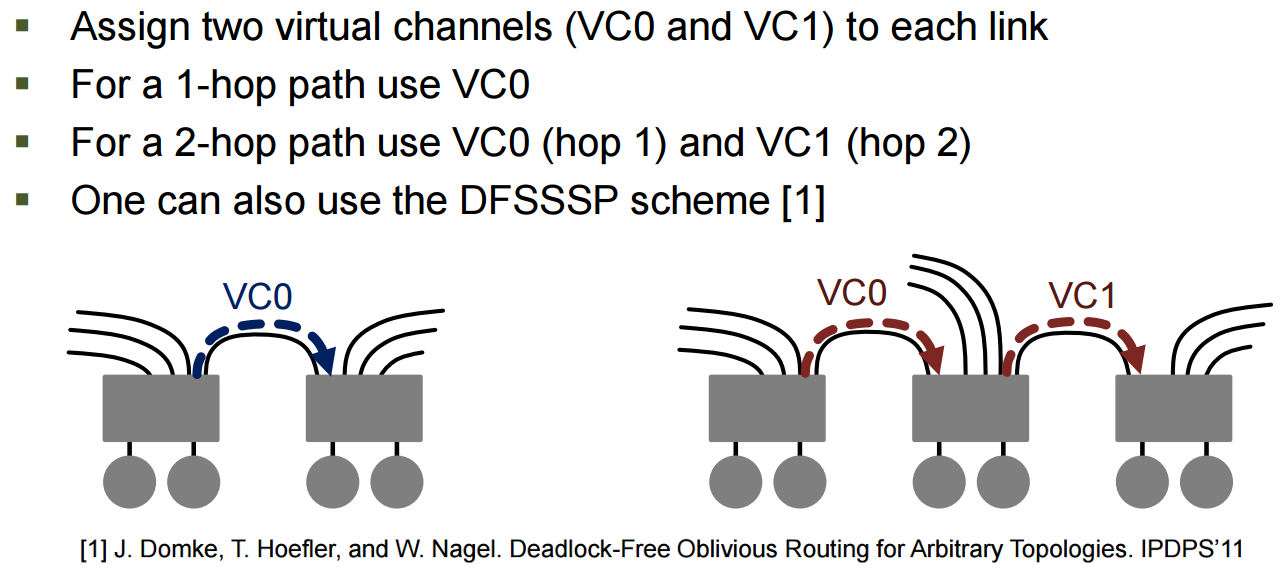
Deadlock-freedom (in minimum static routing).
Download: ready Slim Flies and experiments
| Version | Date | Changes |
| sf.tar.gz | January, 2015 | First release |
The accompanying technical report is in the above archive.
The generated Slim Flies can be found in the subfolder graphs of the archive.
The analyses include cost, bandwidth, resilience, and calculating load per edge in the all-to-all pattern.
Performance experiments were conducted using the Booksim simulator (with a class Anynet). The link:
booksim.
References
| [1] M. Besta, T. Hoefler: | ||
Slim Fly: A Cost Effective Low-Diameter Network Topology
presented in New Orleans, LA, USA, Nov. 2014, Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis (SC14) (acceptance rate: 21%, 82/394) SC14 Best Student Paper (1/82) 


| ||














